
数と数字
どちらも小学校で習う基本的な言葉であるにもかかわらず、その違いを明確に理解している日本人は多くありません。
そもそも2つの言葉の意味の違いを教わる機会はほとんどなく、数学の試験にも、国語の試験にも「数と数字の違いを説明せよ」という問題が出題されることはほとんどありません。
「数は概念であり、数字はその概念を表す文字のことである。または、数はイデアの存在で、数字は形ある存在」
これが答えです。この答えを読んですぐに理解できる人は相当な実力の持ち主です。
筆者がさまざまなところのこの話をすると、きまって相手からポカンとした反応がかえってきます。
「数と数字の違い」という問い自体がはじめてなので、いきなりその答えを知らされても理解が追いつかないのです。
「数字を使える営業マンが数字を作る」
「数字に強い理系、数字に弱い文系」
「視聴率、内閣支持率という数字」
世の中は「数字」であふれています。しかし、本当にそうでしょうか。3つの例文はどれも本来の意味での「数字」の使い方に誤りがあります。
営業マンにとっての数字とは営業成績のことであり、理系が本来強いのは数です。さらに視聴率や内閣支持率は数値です。
かくして、数には「数」と「数字」と「数値」の3つの形態があるのですがその違いは「数字」という言葉に溶けてなくなってしまっているのです。
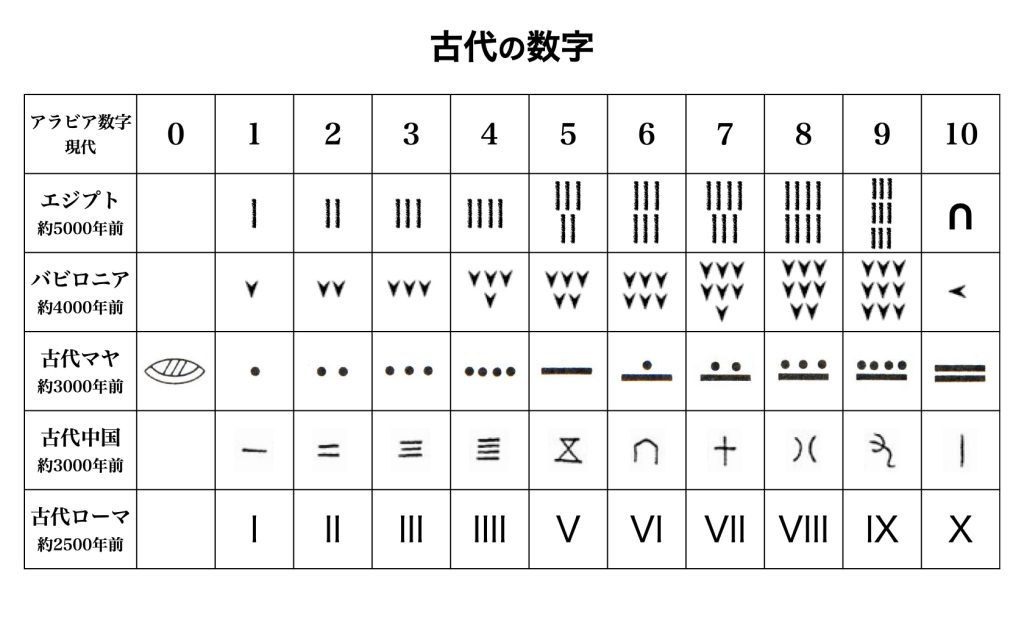
数字の発明
約5000年前のエジプト文明、約4000年前のメソポタミア文明のバビロニア、約3000年前のマヤ文明、約3000年前の黄河文明の古代中国、約2500年前の古代ローマなどでそれぞれ数字が考え出されました。
0,1,2,3,4,5,6,7,8,9というアラビア数字は、もともとインド人によるインド数字がアラビア、そしてヨーロッパに渡り広まり発展してきたものです。ギリシャ数字や漢数字は筆算には適していません。それに対してアラビア数字は筆算するのに適しています。それが十進位取り記数法と「0」という数字をもったアラビア算用数字と呼ばれる所以です。
数字にとってグーテンベルグの活版印刷の発明は決定的でした。それまでの商売や貿易では手書きの数字が用いられていたので、勝手に数字を書き換えられてしまいます。これではまともな商売が安心してできません。活版印刷による印刷された数字は、商取引をはじめ社会全体に大きな影響を与えました。まさにイノベーションだったのです。はたして、アラビア算用数字は世界中に広まっていきました。
▶︎次のページ「数の発見」
次のページへ







